Крок до нейтронних зірок 2. Радіометричне рівняння

Вважайте, що неполяризоване джерело з густиною потоку спостерігається телескопом з еффективною площею , де є геометричною площею телескопа, а є ефективність телескопа. Оскільки кожна з поляризацій складає половину потоку, то густина потужності [] на приймачі є

З іншої сторони, уявімо, що антена є простою резистивною нагрузкою за температури . Хаотичний тепловий рух електронів викликає змінну напругу у цій схемі, що згідно Джонсону-Найквісту має густину потужності , де -- константа Больцмана. Тепер дамо означення температурі антени , як такій, при якій , тоді

де G (gain) є підсиленням антени.

Отже, потік можна замінити температурою . З іншої сторони є температура системи приймання (шум по суті):

де є шумом приймача (приблизно 20 К для систем з охолодженням), є (spillover noise) шумом антени (10 К), виникає через випромінення атмосфери землі, а є фоновим випроміненням небес (CMB, синхротронне випромінювання в площині Галактики) і залежить від точки і частоти спостерігання (10-30К, в центрі Галактики 800К).

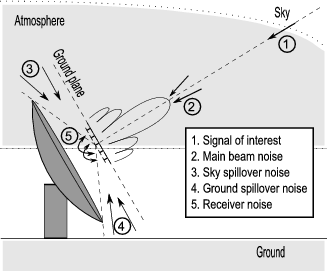
Радіометричне рівняння

Логічно, що щоб сигнал був задетектований, він має бути сильніший флуктуацій шуму в системі приймання. Середньоквадратичне значення флуктуацій є:

де є смуга пропускання приймача, -- тривалість прийому, а є 1 при прийомі в одній поляризації або 2, якщо у двох. Ця формула називається радіометричним рівнянням і є основою основ більшості радіо-асторономічних розрахунків чутливості систем. Давайте ж виведемо радіометричне рівняння для чутливості приймача до імпульсних сигналів.

Най ми маємо пульс з періодом , ширині , та піковій амплітуді , що сидить вище шуму системи . Флуктуації шуму в цьому випадку складаються суми двох частин: коли імпульс є і коли нема :

Справедливо припускаючи, що , маємо:

де -- час спостереження.

Хорошо. Тепер за означенням сигнал/шум є , тоді

Якщо тепер повернутись назад до густини потоку, то середнє значення за період буде:

Цим рівнянням вже можна користуватись. Часом виникає потреба визначити мінімальну густину потоку, що може прийняти радіотелескоп, тоді вводять додатковий корекційний фактор на неідеальність системи

Неідеальності виникають через оцифровування сигналу та інші ефекти. Зазвичай трохи більше одиниці.

Отже чим менше тим слабші пульсари можна спостерігати. З рівняння також видно, що легше спостерігати пульсари з вузькою шириною імпульсів , а якість данних буде тим краще, чим більше час спостереження , чим ширше смуга пропускання приймача. Варто зазначити, що останні два стоять під коренем, тож збільшення часу спостереження в 4 рази, покращить дані лише у 2. Більш ефективно збільшувати підсилення антени та зменшувати шум .

Високе значення сигнал/шум потрібне для надійного підтвердження прийому сигналу пульсара. Професійні астрономи використовують , проте для аматорів вистачить і 4.

Рекомендую почитати Handbook of pulsar astronomy, Lorimer and Framer. Ця стаття є по суті перекладом одного з додатків.